| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 프림 알고리즘
- SERVLET
- greedy
- 그리디
- dbms
- 벡엔드
- programmers
- request
- BJ
- 네이버 부스트캠프 ai tech
- mst
- 웹프로그래밍
- Prim's Algorithm
- 부스트코스
- mysql
- 크루스칼 알고리즘
- 다이나믹 프로그래밍
- 프로그래머스
- 소수
- 웹 프로그래밍
- 순열 알고리즘
- 정렬
- Kruskal's Algorithm
- 해시
- 웹서버
- 정렬 알고리즘
- DP
- 백준
- jsp
- 브라우저
- Today
- Total
끵뀐꿩긘의 여러가지
확률/통계 본문
확률 변수(random variable):
확률현상에 기인해 결과값이 확률적으로 정해는 변수
어떤 변수 $X$를 사용할 때 확률$P(X)$를 구할 수 있다면 $X$는 확률 변수
이산(discrete) 확률 변수: 확률 변수가 가질 수 있는 값의 개수를 셀 수 있는 경우
확률 질량 함수: 이산확률변수에서 특정 값에 대한 확률을 나타내는 함수
$$\mathbb{P}(X \in A) = \sum_{x \in A}p(X = x)$$
연속(continuous) 확률 변수: 확률 변수가 가질 수 있는 값의 개수를 셀 수 없는 경우
확률 밀도 함수: 연속확를변수가 특정 구간에 포함될 확률
$$\mathbb{P}(X \in A) = \int_{A}P(x)dx$$
밀도는 누적확률분포의 변화율을 모델링하며 확률로 해석하면 안된다.
확률분포(probability distribution):
확률 변수가 특정한 값을 가질 확률을 나타내는 함수
데이터는 $(\mathbf{x},y)\sim \mathbb{D}$ 임의의 분포 D분포를 따르는 (x,y) 값으로 표현될 수 있다.
이를 통해, 결합 분포 $P(\mathbf{x},y)$는 $\mathbb{D}$를 모델링하고
$P(\mathbf{x})$는 y 값에 상관없는 $\mathbf{x}$에 대한 주변확률분포를 나타낸다.
또한 조건부 확률 분포 $P(\mathbf{x}|y)$는 입력$\mathbf{x}$와 $y$ 사이의 관계를 나타낸다.
*결합분포: 확률 변수가 여러 개일 때 이들을 함께 고려하는 확률 분포
이산 확률 분포: 이산확률변수의 확률분포
ex. 베르누이 분포, 이항분포, 기하분포, 음이항 분포, 초기하분포, 포아송분포
연속 확률 분포: 연속확률변수의 확률분포
ex. 정규분포, 감마분포, 지수분포, 카이제곱분포, 베타분포, 균일분포
[기초통계] 확률분포의 의미 및 종류
확률 분포의 의미 및 종류
losskatsu.github.io
주변확률분포:
결합확률분포에서 하나의 변수로만 이루어진 확률함수 = 주변확률분포
결합확률분포가 $f(x,y)$ 확률변수 $X$또는 $Y$만의 분포이면
확률변수가 이산확률변수인 경우:
$f_X(x) = \sum_{y}f(x,y)$
$f_Y(y) = \sum_{x}f(x,y)$
확률변수가 연속확률변수인 경우:
$f_X(x) = \int f(x,y)dy$
$f_Y(y) = \int f(x,y)dx$
확률변수 $X$또는 $Y$가 독립이면
$f(x,y) = f_X(x)f_Y(y)$
결합확률(Joint Probability):
사건이 모두 일어날 확률
$$P(A,B) = P(A \cap B)$$
두 사건이 독립이라면,
$$P(A,B) = P(A \cap B) = P(A)P(B)$$
조건부확률(Conditional Probability):
한 사건이 일어났다는 전제 하에 다른 사건이 일어날 확률
$$P(B|A) = \frac{P(A \cap B)}{P(A)}$$
연속확률분포의 경우 $P(y|x)$는 확률이 아니라 밀도이다
기댓값(Expected Value):
어떤 확률을 가진 사건을 무한히 반복 했을 경우 얻을 수 있는 값의 평균으로서 기대할 수 있는 값
이산확률변수의 기댓값:
$$E_{x \sim P(x)}(X) = \sum_{x = \chi}f(x)P(x)$$
연속확률 변수의 기댓값:
$$E_{x \sim P(x)}(X) = \int _{\chi}f(x)P(x)dx$$
기댓값의 성질:

2번은 독립일때 성립
기댓값의 활용:
분산 : $\mathbb{V}(X) = \mathbb{E}_{x \sim P(x)}[(x-\mathbb{E}[x])^2]$
공분산: $Cov(X,Y) = \mathbb{E}_{X_1,X_2 \sim P(X_1,X_2)}[(X_1 - \mathbb{E}[X_1])(X_2 -\mathbb{E}[X_2]) ]$
=>양의 값을 가지면 한쪽이 커질 때 나머지도 증가하는 관계, 음의 값을 가지면 그 반대
상관계수: $corr(X,Y) = \frac{Cov(X,Y)}{\sigma_x \sigma_y}$
=> -1 ~ 1사이의 값을 가지게 되고, +1에 가까울수록 양의 관계가, -1에 가까울수록 음의 관계가 강하다 0에 근접하면 상관관계가 약하다고 본다. 상관계수는 공분산과 달리 크기 비교 가능
첨도 등 여러 통계량을 기댓값을 사용하여 계산할 수 있다.
조건부 분포(Conditional Distribution), 조건부 기댓값(Conditional Expected Value, Conditional mean):
조건부 분포:
$$P(a<Y<b|X = x) = f(y|x) = \frac{f(x,y)}{f_X(x)}$$
$$P(a<X<b|y = y) = f(x|y) = \frac{f(x,y)}{f_Y(y)}$$
조건부 기댓값:
확률 변수 X,Y에 대해서 X = x가 주어져있을 때 Y 값의 기댓값
조건부 기댓값은 조건이 되는 확률 변수의 값에 따라서 값이 달라진다

조건부 기댓값의 예측문제(회귀)에서의 활용:
X = x의 값을 알면 조건부 확률분포 $P(y|x)$의 분포를 알 수 있지만, 가장 대표성이 있는 하나의 값을 정하기 위해서 조건부 확률분포의 기댓값인 조건부 기댓값을 예측 문제의 답으로 하는 경우가 많다. 더 robust한 model을 위해서는 median을 사용하기도 한다.
조건부 기댓값 + 기댓값 정리:
https://analysisbugs.tistory.com/8
[수리통계학] 7. 조건부 기댓값과 조건부 분산
[Ref] 수리통계학 (송명주, 전명식) 안녕하세요, 이번 포스팅에서는 기댓값과 분산 파트의 마지막 부분인 조건부 기댓값과 조건부 분산에 대해서 배워보도록 하겠습니다. 조건부 기댓값은 확률
analysisbugs.tistory.com
몬테카를로 샘플링(Monte Carlo Sampling):
확률분포를 알지 못할 떄 데이터를 이용하여 기대값을 계산하려면 몬테카를로 샘플링 방법을 사용해야한다.
몬테카를로 방법은 독립적으로 무작위 추출된 난수를 활용하여 대수의 법칙에 의거해 그 평균값을 구하는 것이다
ex. 길이가 2인 정사각형 안에 무작위를 점을 찍어서 중심으로부터 길이가 1 이하인 점의 비율을 구한다.
정사각형 넓이 * 1 이하인 점의 비율 $\approx$ 반지름이 1인 원의 넓이

$$\mathbb{E}[f(X)] \approx \frac{1}{N}\sum_{i=1}^{n}f(x^{(i)})$$
import numpy as np
# 몬테카를로 샘플링을 통해서 적분값 구하기
def mc_int(fun, low, high, sample_size=100, repeat=10):
int_len = high-low # 적분 범위
stat = []
for _ in range(repeat):
# 균등분포로 sample_size만큼 [-1, 1] 구간의 x값을 추출한다.
x = np.random.uniform(low=low, high=high, size=sample_size)
# 추출된 이x값으로 높에 해당하는 함수 값을 계산한다.
fun_x = fun(x)
# 밑변과 높이를 곱해 넓이인 int_val을 계산한다.
int_val = int_len * np.mean(fun_x)
stat.append(int_val)
# 구해진 통계량(넓이)를 평균내주면 실제 값과 거의 근사한다.
return np.mean(stat), np.std(stat)
# 구하려는 적분식
def fun(x):
return np.exp(-x**2)
print(mc_int(f_x, -1, 1, 10000, 100))
# 결과
# (1.4939731002894978, 0.003764717448739865* 또 다른 샘플링 방법 MCMC(Markov Chain Monte Carlo)
https://www.secmem.org/blog/2019/01/11/mcmc/
Markov Chain Monte Carlo 샘플링의 마법
이번 포스트에서는 강력한 샘플링 기법 중 하나인 Markov Chain Monte Carlo(MCMC)에 대해 알아보겠습니다. MCMC의 활용도는 굉장히 넓어서 머신러닝을 비롯한 베이지안 통계학, 통계물리학, 컴퓨터비전,
www.secmem.org
http://lifencomputing.blogspot.com/2018/12/sampling-monte-carlo-methods.html
Sampling과 Monte Carlo Methods (몬테 카를로 방법)
Reference 강의자료, 인터넷 여기저기 Gibbs Sampling (by ratsgo, 201705) Sampling 복잡한 확률 모델의 경우, 정확한 확률값을 계산하기 어려울 수 있으므로, 대략적인 값을 구하기 위해...
lifencomputing.blogspot.com
모수적 방법론(Parametric method):
일반적으로 군당 30개 이상으로 구성된 표본의 경우에는 정규분포를 따른다고 가정한다. 그보다 더 적은 표본의 경우 정규성 검정 이후 모수적 방법론을 사용하여야한다
추정량: 모집단에서 뽑은 표본의 통계량
모수: 모평균, 모표준편차, 모분산 등 모집단을 조사하여 얻을 수 있는 통계적인 특성치
유한한 개수의 데이터만 관찰해서 모집단의 분포를 정확히 알아내는건 불가능하므로, 근사적인 확률분포를 추정할 수 밖에 없다.
중심 극한 정리(central limit theorm):
모집단이 평균이 $\mu$이고 표준편차가 $\sigma$ 인 임의의 분포를 이룬다고 할때, 이 모집단으로부터 추출된 표집분포의 크기 n이 충분히 크다면 각 표본 평균들이 이루는 분포는 평균이 $\mu$이고 표준편차가 $\sigma/\sqrt{n}$에 근접한다
이는 모집단이 어떤 분포를 가지고 있던지 간에 표집분포의 크기가 충분히 크다면 표본 평균들의 분포가 모집단의 모수를 기반으로 한 정규분포를 이룬다는 점을 이용하여 표본 분포와 모집단과의 관계를 증명함으로싸, 수집한 표본의 통계량을 이용해 모집단의 모수를 추정할 수 있는 수학적 근거를 만들어준다.
*표집분포(sampling distribution): 하나의 모집단에서 추출할 수 있는 가능한 모든 표본에서 계산된 통계량의 확률분포
모수적 방법론:
중심 극한 정리에 의거하여 데이터가 특정 확률분포를 따른다고 선험적으로 가정한 후 그 분포를 결정하는 모수를 추정하는 방법
- 데이터가 2개의값(0또는1)만 가지는 경우→베르누이분포
- 데이터가 n개의 이산적인 값을 가지는 경우→카테고리분포
- 데이터가 [0,1]사이에서 값을 가지는 경우→베타분포
- 데이터가 0이상의 값을 가지는 경우→감마분포,로그정규분포등
- 데이터가 실수집합 전체에서 값을 가지는 경우→정규분포,라플라스분포등
=> 기계적으로 확률분포를 가정하기보다는 데이터를 생성하는 원리를 먼저 고려하고, 각 분포를 검정하는 것이 중요
모멘트 방법 모수 추정:
표본평균의 평균은 모평균과 같다:
$$\bar{X} = \frac{1}{N}\sum_{i=1}^{N}X_i$$
$$\mathbb{E}[\bar{X}] = \mu$$
참고: 표본평균의 평균이 모평균과 같은 이유
https://hsm-edu.tistory.com/14?category=741767
[손으로 푸는 통계] 3. 표본평균의 평균이 모평균과 같은 이유
고등학교 '확률과 통계'시간에 표본평균의 평균을 모평균과 같다는 것을 배웠는데 증명을 하지는 않습니다. '알려져있다' 라고만 배우는데요. 고등학교 수준의 수학으로 증명 가
hsm-edu.tistory.com
표본분산의 평균은 모분산과 같다:
$$S^2 = \frac{1}{N-1}\sum_{i=1}^{N}(X_i - \bar{X})^2$$
$$\mathbb{E}[S^2] = \sigma^2$$
참고: 표본분산의 평균이 모분산과 같은 이유
https://hsm-edu.tistory.com/15
[손으로 푸는 통계] 4. 표본분산의 기댓값이 모분산과 같은 이유
지난 글에서 표본평균의 기댓값은 모평균과 같다는 것을 보였습니다. 오늘은 표본분산의 평균이 모분산과 같다는 것을 증명해봅시다. 표본에서 구한 어떤 통계량의 기댓값이 모수와
hsm-edu.tistory.com
참고: 불편추정량
https://1992jhlee.tistory.com/19
불편추정량(Unbiased Estimate) - 표본분산은 왜 n-1로 나누나?
통계를 공부하다 보니 굉장히 불편한 것을 하나 만나게 됐다. 그것은 바로 표본에서 분산을 정의할 때 원래 알던 분산의 정의(편차의 제곱의 평균)가 아닌 다른 방식으로 정의한다는 것이다.
1992jhlee.tistory.com
표본 평균의 분산은 모분산 /n이다
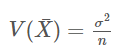
참고: 표본 평균의 분산이 모분산/n인 이유
https://hsm-edu.tistory.com/16?category=741767
[손으로 푸는 통계] 5. 표본평균의 분산이 모분산/n 인 이유(고등학생들 꼭 보세요)
우리는 지난 두개의 글에서 표본평균의 평균이 모평균과 같다는 것과, 표본분산의 평균이 모분산과 같다는 것을 보였습니다. $E(\bar{X})=\mu$ $E(S^{2})=\sigma^{2}$ 표본분산의 평균이 모분
hsm-edu.tistory.com
최대가능도 추정법(Maximum Likelihood Estimation, MLE)(모수적 방법):
가능도 함수(Likelihood function):
가정된 분포에서 주어진 데이터가 나올 가능성인 가능도(likelihood)를 나타내는 함수(가능도는 모두 더해도 1이 나오지 않음)
모수 $\theta$를 따르는 분포가 x를 관찰할 가능성
$$L(\theta;X) = P(X|\theta)$$
동전 던지기 실험의 확률질량함수 - $_{n}\textrm{C}_x p^x(1-p)^{n-x}$ 이항분포
이항분포의 모수 = 동전을 던졌을 때 앞면이 나올 확률 p
동전 던지기 실험을 10번 진행 하였을 때 앞면이 4번 나온 경우
- 확률적으로 해석: 동전을 던졌을 때 앞면이 나올 확률이 1/2이므로, 동전을 10번 던졌을 때 앞면이 4번 나온 경우의 확률
$$P(4) = _{10}\textrm{C}_{4}(\frac{1}{2})^4(1-\frac{1}{2})^6 = 0.1172$$
- 가능도적으로 해석: 동전 던지기 실험이 이항분포를 따른다고 가정하고, 동전을 10번 던졌을 때 앞면이 나올 확률에 따라서 앞면이 4번 나올 가능성
$$L(P;x) = P(x|P) = _{10}\textrm{C}_{4}p^4(1-p)^6 $$

즉, 확률이 0.4일때 이항분포를 따를 가능성이 가장 높다(데이터를 가장 잘 설명한다)
* 다음의 code snippet(단편)은 어떤 확률분포를 나타내는 것일까요? 해당 확률분포에서 변수 theta가 의미할 수 있는 것은 무엇이 있을까요?
import numpy as np
import matplotlib.pyplot as plt
theta = np.arange(0, 1, 0.001)
p = theta ** 3 * (1 - theta) ** 7
plt.plot(theta, p)
plt.show()동전을 10번 던졌을 때 앞면이 3번 나온경우의 이항분포의 가능도함수 => 0.3값이 가장 큰 가능도 함수가 그려질 것이다
확률함수에서는 확률변수가 변수 모수가 인수이지만, 가능도함수에서는 확률변수가 인수 모수가 변수이다.
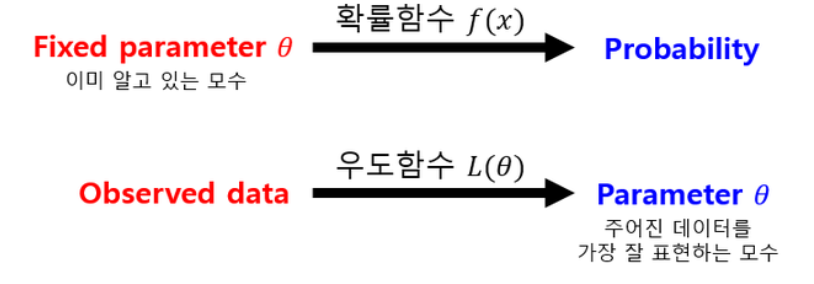
n개의 표본에서의 가능도함수:
독립적으로 추출된 표본이 n개라고 하면($y_1,y_2,\cdots,y_n$) 각 표본들의 확률함수는 전부 $f(Y;\theta)$이고,
가능도함수도 복수 표본값에 따른 결합확률밀도$P_{x_1,\cdots,x_n}(x_1,\cdots,x_n;\theta)$가 된다. 표본 데이터들은 같은 확률분포에서 나온 독립적인 값들이므로 결합확률함수는 다음처럼 곱으로 표현된다
$$L(\theta;y_1,y_2,\cdots,y_n) = \prod_{i=1}^{n}P(\theta|y_1,y_2,\cdots,y_n)$$
로그 가능도 함수:
표본이 여러개일때 가능도함수는 비슷한 함수의 곱으로 나타나므로 로그 변환에 의해 곱을 합으로 바꾸면 연산량이 크게 줄어들게 된다.
경사하강법으로 가능도를 최적화할 때 미분 연산을 사용하는데 로그 가능도를 사용하면 연산량을 $O(n^2)$에서 $O(n)$으로 줄여준다.
$$logL(\theta;y_1,y_2,\cdots,y_n) = \sum_{i=1}^{n}logP(\theta|y_1,y_2,\cdots,y_n)$$
최대가능도 추정법:
주어진 표본에 대해 가능도를 가장 크게하는 모수 $\theta$를 찾는 방법
$$\hat{\theta}_{MLE}= (argmax)_\theta L(\theta;x) = (argmax)_\theta P(x|\theta)$$
*$(argmax)_x(f(x))$ 뜻 $f(x)$를 최대화하는 $x$의 값을 찾는다
최대가능도 추정법 예제 - 정규분포:
정규분포를 따르는 확률변수 X로부터 독립적인 표본 ${x_1,\cdots,x_n}$을 얻었을 때 최대가능도 추정법을 이용하여 모수를 추정하면?
$$\hat{\theta}_{MLE}= (argmax)_\theta L(\theta;x) = (argmax)_\theta P(x|\theta)$$
정규분포의 모수 = $\theta = \mu, \sigma ^2$
로그 가능도를 사용하여 표현하면
$$logL(\mu,\sigma ^2;X) = \sum_{i=1}^{n}logP(x_i|\mu,\sigma ^2;X) = \sum_{i=1}^{n}log\frac{1}{\sqrt{2\pi\sigma ^2}}e^{-\frac{|x_i-\mu|^2}{2\sigma^2}} = -\frac{n}{2}log2\pi\sigma^2 - \sum_{i =1}^{n}\frac{|x_i-\mu|^2}{2\sigma^2}$$
이때 모수의 개수가 2개이므로 각 모수의 편미분이 0이 되는 지점이 가능도의 최대값이다
$$0 = \frac{\partial logL}{\partial \mu} = -\sum_{i=1}^{n}\frac{x_i - \mu}{\sigma ^2} \Rightarrow \hat{\mu}_{MLE} = \frac{1}{n}\sum_{i = 1}^{n}x_i$$
$$0 = \frac{\partial logL}{\partial \sigma} = -\frac{n}{\sigma} + \frac{1}{\sigma^3}\sum_{i=1}^{n}|x_i - \mu|^2\Rightarrow \hat{\sigma}^2_{MLE} = \frac{1}{n}\sum_{i = 1}^{n}(x_i - \mu)^2$$
*카테고리 분포 :
카테고리 확률변수는 1부터 K까지 K개 정숫값중 하나가 나온다. 예를 들어, 주사위는 K = 6인 카테고리 분포이고 눈금이 1이 나왔다면 카테고리 확률변수 $x = (1,0,0,0,0,0)$처럼 원핫 인코딩으로 표시한다.
이에 따라 확률변수의 값도 $x = (x_1,\cdots,x_k)$와 같이 벡터로 표시하고
$$x_i = \left\{\begin{matrix}
0 \\ 1
\end{matrix}\right.$$
$$\sum_{k=1}^{K}x_k = 1$$
의 제한 조건을 가진다.
원소값 $x_k$는 베르누이 확률변수로 볼 수 있기 때문에 각각 1이 나올 확률을 나타내는 모수 $\mu _k$를 가진다.
모수도 $\mu = (\mu_1,\cdots,\mu_K)$ 벡터로 나타나며
$$0 \leq \mu _i < 1$$
$$\sum_{k=1}^{K}\mu _k = 1$$
의 제한 조건을 가진다
카테고리 확률분포는
$$Cat(x_1,\cdots,x_K;\mu _1 ,\cdots,\mu _K) = Cat(x;\mu) = \mu ^{x_1}_1\mu ^{x_2}_2\cdots\mu ^{x_K}_K = \prod_{k=1}^{K}\mu ^{x_k}_k$$
이다.
카테고리 확률변수 $X$에서 $x_1 = 1$이면 나머지는 0이므로 $Cat(x=x_1;\mu) = \mu _1$이다
최대 가능도 추정법 예제 - 카테고리 분포:
카테고리분포 $Cat(x;p_1,\cdots ,p_d)$를 따르는 확률 변수 X로부터 독립적인 표본 ${x_1,\cdots,x_n}$을 얻었을 때 최대가능도 추정법을 이용하여 모수를 추정하면?
카테고리분포의 모수 = p벡터 = $p(p_1,\cdots,p_d)$
$$\hat{\theta}_{MLE} = (argmax)_\theta logP(x|\theta) =(argmax)_{p_1,\cdots,p_d}log(\prod_{i=1}^{n}\prod_{k=1}^{d})p^{x_{i,k}}_k $$
$$log(\prod_{i=1}^{n}\prod_{k=1}^{d})p^{x_{i,k}}_k = \sum_{k=1}^{d}(\sum_{i=1}^{n}x_{i,k})logp_k = \sum_{k = 1}^{d}n_klogP_k$$
$n_k$는 전체 표본에서 k번째 숫자가 나온 횟수
그런데 카테고리 분포의 모수는
$$\sum_{k=1} ^{d}\mu _k = 1$$
을 만족해야하므로, 라그랑주 승수법을 사용하여 로그 가능도에 제한 조건을 추가한 새로운 목적함수를 생성할 수 있다.
$$J = \sum_{k=1}^{K}log \mu _k n_k + \lambda(1-\sum_{k=1}^{K}\mu _k)$$
이 목적함수를 각각의 모수로 미분한 값이 0이 되는 값을 구하면 모수를 추정할 수 있다.
$\frac{\partial J}{\partial \mu _k} = 0, \frac{\partial J}{\partial \lambda} = 0$인 점을 구하면,
$$\frac{\partial J}{\partial \mu _k} = \frac{n_k}{\mu _k} - \lambda = 0$$
$$n_k = \lambda\mu _k$$
$$\frac{\partial J}{\partial \lambda} = 1 - \sum_{k=1}^{K}\mu _k= 0$$
결과 값으로 $\sum_{k=1}^{K} \mu _k = 1$는 카테고리 분포의 모수 제약조건이 나온다
$\lambda$값을 구하기 위해
$$\lambda = \lambda\sum_{k=1}^{K}\mu _k = \sum_{k=1}^{K}\lambda\mu _k = \sum_{k=1}^{K}n_k = N$$
N은 전체 시행 횟수
$$\therefore \mu _k = \frac{n_k}{N} $$
최대 가능도 추정법에 의한 카테고리 분포의 모수는 각 범주값이 나온 횟수와 전체 시행 횟수의 비율이다
딥러닝에서의 최대가능도 추정법:
딥러닝 모델의 가중치를 $\theta = (W^{(1)},\cdots,W^{(L)})$이라 표현했을 때 분류문제의 소프트맥스 벡터는 카테고리분포의 모수 $(p_1, \cdots, p_K)$를 모델링하고, 원핫벡터로 표현한 정답레이블 $y = (y_1,\cdots,y_K)$를 관찰데이터로 이용하여 소프트맥스 벡터의 로그가능도를 최적화할 수 있다.

확률 대신 가능도를 사용하였을 때의 이점은 어떤 것이 있을까요?
확률은 모수의 값이 고정되어있는 반면 가능도는 모수의 변수로 해석되기 때문에 가능도를 사용하면 실제의 값들(표본값들)을 통해서 모집단의 분포를 예측할 수 있다.
연속확률분포에서는 특정 사건이 일어날 확률이 전부 0으로 계산되기 때문에 확률로는 사건들이 일어날 가능성을 비교하는 것이 불가능하다. 하지만 가능도를 사용하면 비교가 가능하다. 연속확률분포의 y 값== 가능도
https://jjangjjong.tistory.com/41
확률(probability)과 가능도(likelihood) 그리고 최대우도추정(likelihood maximization)
* 우선 본 글은 유투브 채널StatQuest with Josh Starmer 님의 자료를 한글로 정리한 것 입니다. 만약 영어듣기가 되신다면 아래 링크에서 직접 보시는 것을 추천드립니다. 이렇게 깔끔하게 설명한 자료
jjangjjong.tistory.com
엔트로피와 크로스 엔트로피
엔트로피:
불확실성의 척도, 어떤 데이터가 나올지 예측하기 어려운 정도
$$H(x) = -\sum_{i=1}^{n}p(x_i)logp(x_i)$$
ex. 동전을 던지는 것보다 주사위를 던지는 것이 엔트로피가 더 높다
모든 경우의 확률이 동일하다면
$$H(x) = -\sum_{i=1}^{n}p(x_i)logp(x_i) = (\sum_{i=1}^{n}p(x_i))(-logp(x_i))= -logp(x_i)$$
이고, $x_i$가 작을수록 $-logp(x_i)$가 커지므로 엔트로피는 증가한다
크로스 엔트로피:
실제 분포 q에 대하여 알지 못하는 상태에서 모델링하여 구한 분포인 p를 통해 q를 예측하는 것.
$$H_p(q) = -\sum_{i=1}^{n}q(x_i)logp(x_i)$$

이진분류에서
y = 0일때 예측값이 1로 갈수록 크로스엔트로피가 증가하고, 예측값이 0이면 크로스 엔트로피가 0이다
y = 1일때 예측값이 0으로 갈수록 크로스엔트로피가 증가하고, 예측값이 1이면 크로스 엔트로피가 0이다
쿨백-라이블러 발산(KL divergence):
기계학습에서 사용되는 손실함수들은 모델이 학습하는 확률분포와 데이터에서 관찰되는 확률분포의 거리를 통해 유도한다.
쿨백 라이블러 발산은 데이터공간에 있는 두 확률 분포 사이의 차이를 계산하는 함수 중 하나이다.(총변동 거리 바슈타인 거리 등이 있음) 어떤 이상적인 분포에 대해, 그 분포를 근사하는 다른 분포를 사용해 샘플링을 한다면 발생할 수 있는 정보 엔트로피 차이를 계산한다.
정답 레이블이 P, 모델예측이 Q일때
이산확률변수에서의 쿨백-라이블러 발산:
$$\mathbb{K}\mathbb{L}(p||Q) = \sum_{x in \chi}P(x)log(\frac{P(x)}{Q(x)})$$
연속확률 변수에서의 쿨백-라이블러 발산:
$$\mathbb{K}\mathbb{L}(p||Q) = \int_{\chi}P(x)log(\frac{P(x)}{Q(x)})dx$$
쿨백-라이블러 발산과 엔트로피&크로스 엔트로피:
$$\mathbb{K}\mathbb{L}(p||Q) = -\mathbb{E}_{x \sim P(x)}[logQ(x)] + \mathbb{E}_{x \sim P(x)}[logp(x)] = -\sum_{c=1}^{C}p(y_c)[log(q(y_c)) - log(p(y_c))] = H_q(P) - H(p)$$
$\therefore$쿨백-라이블러 발산 = 크로스엔트로피 - 엔트로피
쿨백-라이블러 발산의 특징:
$$\mathbb{K}\mathbb{L}(p||q) >0$$
크로스 엔트로피의 lower bound가 엔트로피 값이기 때문에 언제나 0보다 크다
$$\mathbb{K}\mathbb{L}(p||q) \neq \mathbb{K}\mathbb{L}(q||p)$$
크로스 엔트로피는 asymmetic하므로 거리개념이 아니다
확률 분포 사이의 거리(쿨백-라이블러 발산)를 최소하는 개념과 로그 가능도를 최대화한다는 개념은 굉장히 밀접하게 연관되어있다.
비모수적 방법론(Parametric method):
정규성 검정(데이터셋 분포가 정규분포를 따르는지 검정)에서 정규성을 따르지 않는다고 증명되거나 군당 10개 미만의 소규모 분포에서는 정규분포임을 가정할 수 없으므로 모수적 방법을 사용할 수 없다.
부호검정, 윌콕슨 순위합 검정, 분호순위합검정 등을 사용한다
혼동행렬(Confusion Matrix) & 오류 & 분류성능평가지표:
혼동행렬:

1종 오류: 귀무가설 $H_0$가 실제로는 참이어서 채택해야 함에도 불구하고 채택되지 않은 오류 = $\alpha$
유의수준: 1종 오류를 범할 확률의 허용 한계
2종 오류: 귀무가설 $H_0$가 실제로는 거짓이라서 채택하지 말아야하는데 채택된 오류 = $\beta$
정확도(acuuracy): $\frac{TP + TN}{FN+TP+FP+TN} $
정밀도(precision): 예측을 True로 한 것들중에 실제 True인 것 $\frac{TP}{TP+FP} $
민감도(sensitivity),재현율(recall): 실제 True인 것들 중에 예측을 True로 한 것 $\frac{TP}{TP+FN} $
특이도(specificity): 실제 False인 것들중에 에측을 False로 한 것 $\frac{TN}{FP+TN} $
베이즈 정리(Bayes Theorem):

evidence: 전체 데이터의 분포
가능도: 원래 모수($\theta$)에서 새로운 데이터 D가 관측될 가능성
사전확률을 가능도와 Evidence를 사용하여 갱신하여 사후확률을 계산한다
베이즈 정리에 대한 관점: 확률을 빈도주의적으로 바라보지 말고, '주장에 대한 신뢰도'로 생각할 것
사전확률: evidence를 관측하여 갱신하기 전 내 주장에 대한 신뢰도
사후확률: evidence를 관측하여 사전확률을 갱신한 내 주장에 대한 신뢰도
=> 귀납적 추론 방법
베이즈 정리 예제1:
질병 A의 발병률은 0.1%로 알려져있다. 이 질병이 실제로 있을 때 질병이 있다고 검진할 확률(민감도)은 99%, 질병이 없을 때 없다고 실제로 질병이 없다고 검진할 확률(특이도)는 98%라고 하자.
만약 어떤 사람이 질병에 걸렸다고 검진받았을 때, 이 사람이 정말로 질병에 걸렸을 확률은?
문제의 혼동행렬:

사전확률 $P(H)$ = 0.001, 민감도 $(E|H)$ = 0.99, 특이도$P(E^c|H^c)$ = 0.98이므로 베이즈 정리를 사용하면
$$P(H|E) = \frac{P(E|H)P(H)}{P(E)} = \frac{P(E|H)P(H)}{P(E|H)P(H) + P(E|H^c)P(H^c)} \approx 0.047$$
베이즈 정리 예제2:
예제 1에서 한 번 양성 판정을 받았던 사람이 두 번째 검진을 받고 또 양성 판정을 받았을 때, 이 사람이 실제로 질병에 걸린 확률은?
베이즈 정리는 신뢰도를 갱신해 나가는 방법이므로 예제 1의 사후확률이 사전확률로 이용되어서 다시 한번 더 갱신된 사후확률을 계산해준다
문제의 혼동행렬:


심슨의 역설(Simpson's paradox):
각 부분에 대한 평균이 크다고 해서 전체에 대한 평균까지 크지는 않다

인과관계(causality) 추론과 조건부확률:
인과 관계는 데이터 분포의 변화에 강건한 예측모형을 만들 때 필요하다
조건부 확률은 유용한 통계적 해석을 제공하지만 인과관계를 추론할 때 함부로 사용해서는 안된다
인과 관계를 알아내기 위해서는 중첩요인(confounding factor)의 효과를 제거하고 원인에 해당하는 변수만의 인과관계를 계산해야한다
그렇지 않으면 가짜 연관성(spurious correleation)이 나타나게 된다

$$P(y|do(x)) \neq P(y|x)$$
$do(x)$:x를 통제하여 중첩요인(Z)이 주는 영향력을 제거하면,
모든 환자가 의약품을 사용하였다고 가정하였을 때의 회복할 확률
($\sum_{z \in {male, female}}P(Y = 1 | X = O,Z=z)P(Z = z) $)과
모든 환자가 의약품을 사용하지 않았다고 가정하였을 때의 회복할 확률
($\sum_{z \in {male, female}}P(Y = 1 | X = \times,Z=z)P(Z = z) $)을 비교할 수 있고
이는 Y와 X의 인과관계를 나타낸다.
'Naver boostcamp -ai tech > week 01' 카테고리의 다른 글
| 주피터 노트북 단축키/명령어/디버깅 (0) | 2022.09.24 |
|---|---|
| 경사하강법 (1) | 2022.09.22 |
| 선형대수학 (1) | 2022.09.22 |
| pandas (0) | 2022.09.21 |
| Numpy (1) | 2022.09.21 |


