| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- SERVLET
- request
- Prim's Algorithm
- 벡엔드
- 네이버 부스트캠프 ai tech
- programmers
- jsp
- BJ
- 그리디
- 프림 알고리즘
- 브라우저
- dbms
- 백준
- mst
- 정렬 알고리즘
- 프로그래머스
- DP
- 해시
- Kruskal's Algorithm
- 순열 알고리즘
- 웹 프로그래밍
- 웹서버
- 웹프로그래밍
- 부스트코스
- 크루스칼 알고리즘
- 정렬
- greedy
- mysql
- 소수
- 다이나믹 프로그래밍
- Today
- Total
끵뀐꿩긘의 여러가지
1강- 확률과 셈 원리 (Probability and Counting) 본문
1강- 확률과 셈 원리 (Probability and Counting)
끵뀐꿩긘 2022. 9. 25. 03:49
Statistics is the logic of uncertainity
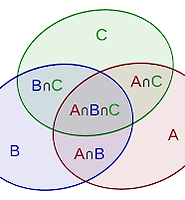
표본공간(sample space): 시행에서 발생가능한 모든 경우의 집합
사건(event): 표본공간의 부분집합
확률의 naive한 정의:
$$P(A) = \frac{num.\; of\; favorable\; outcomes}{num.\; of\; possible\; outcomes}$$

assume:
- 모든 사건이 발생할 확률이 같다(ex. 화성에 생명체 존재? 있다 없다 2가지 경우의 수이므로 확률 =1/2 => (X))
- 유한한 표본공간
=> 항상 이 가정이 만족되는 것은 아니므로 적용 불가한 경우가 있다
셈 원리(Counting Principle):
곱의 법칙(Multiplication Rule): 발생가능한 경우의 수가 각각 n_k가지인 K번의 시행에서 발생 가능한 모든 경우의 수는
$\prod_{k=1}^{K}n_i$이다
이항계수(Bionomial Coefficient):
$$_{n}\textrm{C}_k = \binom{n}{k} = \frac{n!}{(n-k)!k!}$$
Sampling Table: n개 중에서 k개 뽑기
| Order | |||
|---|---|---|---|
| matter(순서 상관 있음) | no-matter(순서 상관 없음) | ||
| replacement | T(복원추출) | $$_{n}\Pi _{k}$$ | $$_{n}\textrm{H}_k$$ |
| F(비복원추출) | $$_{n}\textrm{P}_k$$ | $$_{n}\textrm{C}_k$$ | |
$_{n}\textrm{P}_k$: 순열(Permutation)
$$_{n}\textrm{P}_k = n(n-1)\cdots(n-k+1) = \frac{n!}{(n-k)!}$$
$_{n}\Pi _{k}$: 중복순열(Permutation with repetition)
$$_{n}\Pi _{k} = n^k$$
$_{n}\textrm{C}_k$: 조합(Combination)
$$_{n}\textrm{C}_k = \frac{n(n-1)\cdots(n-k+1)}{k!} = \frac{n!}{(n-k)!k!}$$
$$_{n}\textrm{H}_k$$: 중복 조합(combination with repetition)
$$_{n}\textrm{H}_k = _{n+k-1}\textrm{C}_k = _{n+k-1}\textrm{C}_{n-1}$$
중복조합 공식 이유:
https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=baboedition&logNo=220933436576
7강. (확률-3) 셀수 있는 확률, 중복조합
안녕하세요. 너무 친절한 콩수학입니다~ 콩수학 강의는 수능기출문제풀이와 중요개념정리로 구성되어 있어...
blog.naver.com
'Naver boostcamp -ai tech > Statistics 110' 카테고리의 다른 글
| 6강- Monty Hall 문제와 심슨의 역설 (Monty Hall, Simpson's Paradox) (1) | 2022.10.11 |
|---|---|
| 5강- 조건부 확률과 전확률정리 (Conditioning Continued, Law of Total Probability) (0) | 2022.10.10 |
| 4강- 조건부 확률 (Conditional Probability) (0) | 2022.10.04 |
| 3강- Birthday Problem과 확률의 특성 (Birthday Problem, Properties of Probability) (0) | 2022.10.04 |
| 2강- 해석을 통한 문제풀이 및 확률의 공리 (Story Proofs, Axioms of Probability) (0) | 2022.09.28 |